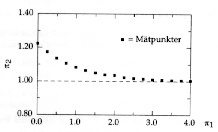
Diagram 1. Uppmätta data på dimensionlös form. Den streckade
linjen markerar asymptoten 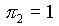
Försöket utfördes med en kopp espresso av av normal styrka
och begynnelsetemperatur enligt ovan.
Resultatet visas i diagram 1.

Diagram 1. Uppmätta data på dimensionlös form. Den streckade
linjen markerar asymptoten 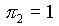
I diagram 1 ser vi att kurvan går mot 1 för stora
 , dvs. stora tider. Kurvan ser dessutom ut
som en exponentialfunktion med negativ exponent. Vi antar alltså att
kurvan kan beskrivas av funktionen
, dvs. stora tider. Kurvan ser dessutom ut
som en exponentialfunktion med negativ exponent. Vi antar alltså att
kurvan kan beskrivas av funktionen

där  och
och 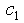 är
okända, dimensionslösa konstanter. Då
är
okända, dimensionslösa konstanter. Då
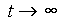 , alltså
, alltså 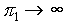 ,
ser vi ur diagrammet att
,
ser vi ur diagrammet att  . Detta innebär
att
. Detta innebär
att 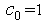 i sambandet (4) ovan. Vidare ser också
att då t = 0, dvs.
i sambandet (4) ovan. Vidare ser också
att då t = 0, dvs.  , så
är
, så
är 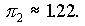 . Detta innebär att
. Detta innebär att
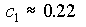 i (4).
i (4).
Funktionen som beskriver espressons kallnande kan alltså vara

där 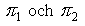 ges av ovan.
ges av ovan.
För att kontrollera om sambandet är korrekt lineariseras (5). Då
fås

Vänsterledet i ekvation (6) plottas mot högerledet i samma ekvation, se diagram 2.
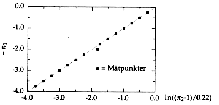
Diagram 2. Den lineariserade ekvationen (6)
Vi ser ur diagram 2 att resulatet faller på en rät linje, streckad i diagram 2. Detta stämmer överens med ekvation (6) och sambandet (5) är alltså korrekt. Det kan noteras att den avvikande mätpunkten troligen härrör från ett mätfel.

