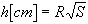
av
Väg- och vattenbyggnad
Tekniska Högskolan i Luleå
Det mesta är skrivet inför en kurs i december 1993 för de entreprenörer i Pite Älvdal som arbetar med isbanor för biltestning. Projektet har finansierats av stiftelsen COLDTECH.
Luleå i maj 1994
Lennart Fransson
Om man ställer en hink med vatten utomhus i kyla kommer allt vatten så småningom att frysa till is. Isen bildas först som ett tunt genomskinligt skal runt vattenvolymen mot hinken och vid vattenytan och växer sedan radiellt in mot mitten. När en vattendroppe fryser mot en kall glasskiva förvandlas den snabbt till is. Genom ett mikroskop ser man att gränsen mellan is och vatten har ett fingerliknande sicksack mönster. Vid omvandlingen från flytande till fast fas frigörs små gasbubblor som hastigt krymper. Mot slutet är vattnet innestängt i ett tunt isskal som sprängs vilket orsakar kraftig turbulens och bubbelbildning. I den frusna vattendroppen lämnas tydliga spår som visar frysriktning, fryshastighet och graden av övertryck vid bildandet. Vattenrörelser, gravitation, tryck och temperaturgradient påverkar isens slutliga kvalitet.
Det värme som avges då vatten övergår till is (334 kJ/kg) transporteras i riktning mot kallare punkter ut till luften. Värmeflödet är proportionellt mot temperaturskillnaden mellan två närliggande punkter längs vägen. Därför växer isen fort i början varefter hastigheten avtar som ett resultat av den isolerande effekten av den redan bildade isen. Omvandlingen av vatten till is följs av en volymökning som får till följd att trycket i det innestängda vattnet ökar. Trycket blir snabbt tillräckligt för att bryta isytan varpå vatten strömmar ut. Den is som då bildas blir mjölkfärgad och porös. Vill det sig illa kan även hinken sprängas. Detta kan enkelt förhindras genom att lägga på ett isolerande lock som reducerar istjockleken på ytan så att den lättare brister.
Is består av samma grundämnen som vanligt vatten H2O, alltså väte och syre. Naturlig is består i regel av många iskristaller ibland mindre än 1 mm och ibland meterstora. Varje enskild iskristalls geometriska struktur är hexagonal där syreatomer och vätebindningar bildar regelbundna sexhörningar. Dessa sk basplan staplas på varandra med ett bestämt avstånd på ca 7.37 Å (1 mm = 10 miljoner Å). Kristallens huvudsymmetriaxel kristallaxeln är vinkelrätt mot basplanen. I en iskristall sammanfaller kristallaxeln med den riktning i vilken polariserat ljus helt utsläcks. Genom att vrida ett tunnskuret isprov i korspolariserat ljus kan således kristallaxeln för varje ingående iskristall fastställas.
Genom mätning av atomgittrets geometri med röntgen-diffraktion kan man teoretiskt beräkna isens densitet. Densiteten för ren is vid noll grader blir då 916.6 kg/m3 med måtten enl figuren vilket stämmer bra med vägning.
Iskristallen har olika egenskaper i olika riktningar. När det gäller de mekaniska egenskaperna kan man likna is med en stapel av spelkort med dåligt lim mellan korten. Limmet motsvaras av basplanen och kristallaxeln går i stapelns höjdled. Stapeln går lätt att förskjuta i sidled men håller bra för en vertikal last. För is som innehåller många kristaller är egenskaperna till stor del kopplade till de ingående kristallernas orientering, men kristallernas storlek och form har också stor betydelse.
Istillväxtens hastighet beror väsentligen på avkylningen från luften eller mer korrekt den bildade isens värmeledning uppåt.
Med hjälp av ledningsekvationen kan man visa att istjockleken är proportionell mot summan av dygnsmedeltemperaturen. Istjockleken h ges av
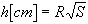
där S är summan av negativa grader ggr dygn efter isläggningsdatum och R är en konstant (R= 2.2 ger rimliga värden för kärnis).
Om det blåser eller snöar vid den första isbildningen kommer det tunna isskiktet att få ett annat utseende. I stället för klara skivor bildas isnålar, sönderblåsta ishinnor och snöblandad is. Detta påverkar i sin tur den underliggande kärnisen. Kristallerna blir som smala pinnar (1-10 mm) vilket gör isen segare och mindre känslig för temperaturväxlingar. Snöinblandning i de översta skiktet medför även något långsammare istillväxt.
Fortsatt snöfall leder så småningom till att det flytande istäcket pressas ner i vattnet. Vatten kan då börja strömma upp (t.ex. genom landsprickor) och sprids lätt över ett stort område. Vattnet sugs upp en bit i snön (varierar med snötyp och temperatur) varefter den vattenblandade snön kan börja frysa uppifrån och ner mot den underliggande isen. Den mjölkfärgade istyp som då bildas kallas stöpis. Egenskaperna varierar kraftigt främst beroende på luftinblandningen och storleken på luftbubblorna. Kristallerna är många och små (ca 1 mm) vilket gör isen segare och förhållandevis stark. Under förutsättning att stöpisen har frusit ordentligt samman med underliggande is bidrar den till en förhöjd bärförmåga. Ofryst snö-is blandning kallas stöp. Så länge det finns ofrusen stöp i isen kan det inte ske någon istillväxt under kärnisen.
Vid hög belastningshastighet och måttliga belastningar kan is möjligen idealiseras som ett linjärt elastiskt material. Det innebär att en provstav av is förlängs proportionellt mot den last som påförs. Sambandet mellan kraft per areaenhet och töjning ges av elasticitetsmodulen. Den är för kärnis ca 8000 MN/m2 vilket innebär en töjning på 1 mm per 10 meter is om en kvadratmeter is belastas med 0.8 MN (80 ton). Den last vid vilken isen brister är ett mått på dess hållfasthet och den då erhållna töjningen är ett mått på isens töjbarhet.
För långsamma belastningar måste man ta hänsyn till att isens deformationer ökar med tiden trots att lasten inte ökas. Denna tidsberoende deformation ökar då lasten närmar sig isens maximala bärförmåga. Här spelar temperaturen en viktig roll. Kärnis som närmar sig smältpunkten deformeras till stor del genom att kristallerna glider isär. Ytterst små föroreningar i vattnet (t.ex salt) sänker smältpunkten och därmed ökar deformationerna jämfört med ren is vid samma temperatur.
Kall is är ett sprött material och dess hållfasthet påverkas i hög grad av inbyggda felaktigheter i kristallerna eller tidigare uppkomna småsprickor. Känsligheten för att sådana sprickor ska leda till ett materialbrott mäts genom att belasta delvis spräckta isprov till brott. Den då erhållna lasten i förhållande till en teoretisk funktion av spricklängden kallas brottseghet vilket kan jämföras med hållfastheten för att få en uppfattning om hur spröd en viss istyp är vid en viss temperatur. Provets storlek är härigenom av största betydelse. Man kan baserat på linjär brottmekanik förvänta sig att isen blir allt sprödare med ökande dimension. Belastningshastigheten påverkar också den uppmätta hållfastheten dels genom att den tidsberoende deformationen fram till brott blir olika och dels genom att antalet sprickor som hinner bildas före brott blir olika. Därför måste även en ingenjörsmässig bedömning av isens hållfasthetsegenskaper göras med största eftertanke så att istyp, dimensioner, temperatur och provets belastningshastighet efterliknar det verkliga förhållandet. Om så inte är fallet hamnar man lätt i en gungfly där de teoretiska beräkningarna har mycket liten tillförlitlighet.
Mellan dessa stora sprickor finns många torra sprickor med varierande sprickvidder från hårfina till centimetervida. Ett mått på ett tjockt istäckes innehåll av torrsprickor utgörs av den fria termiska längdutvidgningen. Genom att mäta temperatur och tryck i ett istäcke kan man påvisa att det för ett snöfritt istäcke ofta krävs en temperaturhöjning på ca 5° för att trycket ska öka. Det motsvarar ca 25 mm total sprickvidd per 10 meter islängd. Dessa sprickor påverkar isens hållfasthet mer eller mindre negativt beroende på belastningens riktning.
Ett allvarligare fall av deformation av is är bildandet av råkar. En råk består av ett brutet istäcke där två istäcken har tryckts ihop. Den pådrivande kraften kan antingen vara temperatur (mindre sjöar och strandnära) eller vind (öppna vidder). Eftersom våta sprickor cementeras med ny is växer den sammanlagda isytan under året. Isen expanderar mot svaga zoner som får härbärgera övertalig is. I Lule skärgård kallas nedåtråkar "fall". Till havs bildas ofta stora isvallar på 20 m och mer som i Bottenviken kallas stampvallar.
Om luften eller vattnet blir varmare än isens fryspunkt börjar den långsamt att smälta. Solstrålning är än värre eftersom värme då kan fångas upp djupt nere i isen. Kärnisen blir då svart och smältpölar bildas. Smältvattnet eroderar snabbt kristallgränserna och isen blir så småningom helt vattengenomsläpplig. Man säger att isen flyter upp. Isen är nu ganska murken men om den är tjock och vit bär den fortfarande. Då isen återigen blir mörk är bärförmågan helt slut. Isen är genomrutten och faller lätt sönder i tusentals isnålar. Det är under sådana sena vårperioder som man kan förledas att bege sig ut på en is som endast hålls ihop av den tunna is som bildats på ytan under en kylig natt. Dagsmejan kan bli ödesdiger.
- isen kan frysa både uppifrån och nerifrån
- ofruset vatten kan bli innestängd mellan två skikt
- vidhäftningen mellan skikten kan bli ofullständig
Fryshastigheten och vattnets luftinnehåll påverkar i hög grad den slutliga kvaliteten på den uppspolade isytan. Snabb istillväxt ger en fin och jämn fördelning av gasbubblor medan långsam istillväxt medför att bubblorna i vattnet blir större och kan genom ytspänning stötas undan vid istillväxten. Genom att använda varmt vatten kan man få en viss uppsmältning av ismodd och även en lägre lufthalt.
Det är svårare än många tror att få en isyta liknande inomhusbanor genom enbart naturlig frysning. Orsaken till dålig ytjämnhet kan vara
- vattenläckage under frysperioden
- uppflytning av ispartiklar
- ojämnt underlag
- bågnande underlag
- nederbörd eller snödrev
- vattenläckage genom den nybildade ytan
- ojämnt vattenflöde och dålig vätning
Grunden för ett lyckat resultat läggs genom att sopa isytan noggrant före bevattningen. Då det är mycket kallt är det bra att förbehandla ytorna med ett tunt lager vatten som snabbt sprejas över.
Den påspolade isen är förhållandevis mer känslig för solstrålning än den naturliga isen. Den mjuknar snabbare och förlorar snabbt den jämna överytan. Detta beror på att den innehåller mycket luft och är skiktad så att solstrålarna fångas in i de övre skikten. Uppvärmningen ökar drastiskt om smältvattnet hinner värmas upp innan det dränerats bort.
Is kan alltså armeras ungefär som betong genom att lägga in trä-stänger. Ett naturligt istäcke kan armeras uppifrån med ett rutnät av sågat virke som vattnas in. I de experiment som utfördes vid LuTH kom vi fram till att ca 1 % relativ armeringsarea var lämpligt för att få en ökning av bärförmågan. Den armerade isen får också en mycket stor seghet som gör att det finns tid att sätta sig i säkerhet om isen överbelastats.
Is kan också armeras genom att blanda in träfiber i vattnet. Därigenom uppnår man en större hållfasthet och ett segare material. Vid solstrålning bildar sågspån och liknande träfiber en utmärkt isolering för den underliggande isen. Ett praktiskt sätt att tillverka fiberarmerad is kan vara att blanda sågspån med snö med en snöslunga. Blandningen kan sen packas med väghyvel och bevattnas och packas igen.
Översiktsbild av försöksområdet.
För oss som inte kan hoppas på under, är följande utveckling på tunn is mer trolig: När vi ökar lasten kommer isen att böja sig så pass att vi hör ljudet av radiell uppsprickning. Detta innebär normalt inte total kollaps av istäcket. De radiella sprickorna är i början torra men öppnas alltmer underifrån. Ökar vi lasten ytterligare kommer ringsprickor att slå upp. Dessa sprickor och alla andra våta sprickor innebär omedelbar risk för kollaps. Enda möjligheten att rädda situationen är då att fördela ut lasten på en större yta genom att t.ex lägga sig ner. Skulle inte det hjälpa återstår bara den flytkraft som det iskalla vattnet kan erbjuda. Det är oväntat svårt att själv ta sig upp på en såphal och bågnande is. Sådana övningar har ofrivilligt ingått i min träning för överlevnad men jag avstår gärna i fortsättningen.
- använd en ispik för att slippa bli blöt
- bär isdubbar om livet är dig kärt
Man lär sig snabbt vilket motstånd som krävs för en viss ispik för att isen ska vara bärkraftig. Fem centimeter kärnis av god kvalitet brukar räcka för mig (ca 80 kg) men jag känner mig betydligt tryggare om isen är tjockare. Den genomskinliga kärnisen är speciell eftersom man vid varje nybildad torrspricka kan se och bedöma tjockleken. Den tunna kärnisen har också ofta en ofattbar jämnhet. Is som har bildats vid snöfall är däremot nyckfull och "soppig" speciellt om det är varmt. Då räcker inte ens 10 centimeter för att man ska kunna känna sig trygg.
På provningssidan råder globalt en stor likriktning av den isforskning som bedrivs. Många universitet ägnar all sin kraft att studera någon form av egenhändigt tillverkad is och övriga försöker utveckla småskalig fysisk modellering. Många experiment (en gång och aldrig mer) görs av personer som normalt studerar helt andra material. Allmänt anses isforskningen som en aning exotisk och knyts därför till polarexpeditioner av olika slag. Den sprödaste isen undviker man ofta att prova om resultatet från traditionell provning visar en besvärande stor spridning.
Med de nya provmetoder som finns i dag är det möjligt att testa all sjöis och annan is så att resultatet kan användas i numeriska modeller. De variabler som man måste brottas med är framför allt temperatur, riktningsberoende och luftinblandning.
1. mätning i borrade hål
2. mätning med infrusen värmetråd
3. indirekt genom mätning av gångtider med markradar
Metoden att mäta tjockleken i ett borrat hål kan allmänt rekommenderas och kräver ingen närmare förklaring. I varmt väder är det dock inte tillrådligt att borra stora hål utan att täta dem med t.ex en träplugg. Dessa hål eroderar då snabbt så att bärförmågan äventyras. En infrusen värmetråd ger ett exakt värde i en och samma punkt. Tråden ger en minimal störning och lämpar sig därför bra för beräkning av istillväxt.
Markradar är troligen det bästa alternativet som erbjuds för att kunna mäta istjocklek längs en lång isväg. Radiovågor med olika våglängder delar upp sig i olika reflekterade vågor som kan detekteras vid isytan. En typ av vågor reflekteras mot isytan och en annan vid gränsskiktet mellan is och vatten. Metodens svaghet är att även en tunn vattenyta eller fuktig snö ger en kraftig dämpning och således en svag signal från isbotten. Utrustningen måste alltid kalibreras mot ett antal kända istjocklekar längs vägen eftersom gångtiden i isen varierar med temperatur och salthalt.
För att kunna följa istillväxten kontinuerligt på ett visst ställe under en längre tid har jag testat en automatisk mätmetod. Det hela går ut på att mäta temperaturskillnaderna mellan minst två punkter i isen med termotråd. Genom att utnyttja använda enkla beräkningsmetoder stämde det ganska bra med direkt istjockleksmätning (metod 2). Det är också möjligt att med hjälp av väderleksprognoser uppskatta en trolig framtida istillväxt.
Med en vanlig utomhustermometer kan man enkelt mäta isens temperatur i ett torrt borrhål som tätas med snö. Om man använder en distanstermometer med en liten givare kan man borra ett ca 5 mm hål med en metallborr. Vill man bestämma en hel temperaturprofil genom ett tjockt istäcke fungerar det bäst om man tar upp en iskärna där man snabbt mäter längs en måttsatt linje några cm in från ytan. Temperaturens variation med tiden mäts bäst genom att frysa in en temperaturgivare i isen. Genom att också mäta vattnets temperatur alldeles under isen får man en kalibrering till noll grader på köpet.
Vi antar att isen brister (böjdragbrott) för en viss kritisk krökning. Detta är ett rimligt antagande om lasten fördelas ut på en tillräckligt stor yta och pålastningen sker snabbt. På dåliga vårisar sker brottet i regel som en genomstansning och då duger inte denna metod. Genom provning för olika istjocklekar har någon föreslagit formeln
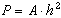
där P är lasten i kg och h är istjockleken i cm. Konstanten A finns angivet i svensk och utländsk litteratur, se tabell 1. I instruktionsboken för Röda Armén föreslås A=7.0 för hjulfordon och A=12.3 för bandfordon. Här finns en viss säkerhetsmarginal inräknad. Formeln tar ingen hänsyn till lastutbredningen men den återspeglas ändå i viss mån genom att olika värden på A föreslås. Om beräkningen ska gälla för dåliga isförhållanden bör det finnas tillfällen då betydligt större last är möjlig. I en krigssituation är det troligt att andra konstanter skulle föreslås. De svenska försök som utförts av Armén och LuTH har visat att A=10 medför en viss risk för genombrott för varma isar. Inverkan av fordonets hastighet och inverkan av upprepade belastningar har inte tagits med i beräkningen. Resultaten kan troligen endast användas för att beräkna bärförmåga för lättare fordon och för istjocklekar mellan 10 och 70 cm.
Tabell 1.
---------------------------------------------------------------------
Källa Last, istyp A (kg/cm2)
---------------------------------------------------------------------
Koronov(1) och Peschanskii(1) 10
---------------------------------------------------------------------
Lebedev(1) och Zubov(1) 16
---------------------------------------------------------------------
Instruktioner till hjulfordon 7.0
Röda Armén(1) bandfordon 12.3
---------------------------------------------------------------------
Lysukhin(1) hjulfordon 8.2
bandfordon 12.3
---------------------------------------------------------------------
Sundberg-Falkenmark (1963) nollgradig sjö-is 10
Fransson (1984) varm skärgårds-is 10
---------------------------------------------------------------------
(1) Uppgifterna som är hämtade ur en litteraturundersökning av Kerr (1975) avser ryska experimentella resultat.
Genom en rad experiment med olika lastutbredningar och iskvaliteter föreslog Panfilov (1960) att isens maximala bärförmåga vid snabb pålastning P beräknas enligt
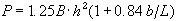
där B är ett uppmätt indexvärde på
böjhållfastheten för en isbalk utskuren ur den aktuella isen
och b är lastens utbredning. Isens karakteristiska
längd L ges av L =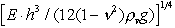 
,
där isens tjocklek h och elasticitetsmodul E (kan
bestämmas med balkprovet) ingår som variabler.
Tvärkontraktionstalet 
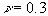, vattnets densitet
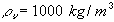och gravitationen g = 9.81 m/s2antas vara
konstanter. Elasticitetsmodulen kan även väljas som en konstant
E= 4500 MN/m2 (rekommenderas för en stor volym kärnis vid noll grader) eftersom den inte har så stor inverkan
på L. Med dessa förenklingar får vi
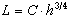
där C är en konstant som kan bestämmas genom elastisk nedböjning av den aktuella isytan med en relativt liten last. Med ovan antagna konstanter blir
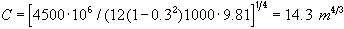
Vid punktbelastning av ett jämntjockt istäcke erhålls
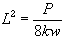
där P är lasten, w är elastisk nedböjning och k=9810 N/m3.
Observera! Det finns nu ingen säkerhetsmarginal. Det här är ett försök att förutsäga den mest troliga lasten som medför att isen brister helt och hållet. Metodens nackdel är att det krävs en tidsödande provning av den aktuella isen. Helst skulle man önska sig statistik från många års provningar där resultatet kopplades till isens tidigare "levnadshistoria". Extrema temperaturer och belastningar måste då räknas som historiskt intressanta händelser.
Den kraftigare vågbildningen i istäcket som uppkommer vid den kritiska hastigheten orsakar en starkare krökning i förhållande till det statiska fallet (låg hastighet). Teoretiskt kan våghöjden växa kaotiskt vid resonans. Experimentellt har man dock som mest uppmätt ca 3 gångers förhöjning vilket ger ett mått på is-vatten-systemets goda dämpning. Genom att fordonet rör sig i riktning mot obruten is är det fullt möjligt att allvarligt skada isen genom en olyckligt vald hastighet utan att själv förolyckas. Genom att avsiktligt anlägga en krokig isväg kan man effektivt begränsa hastigheten.
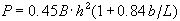
då lasten placerades nära en fri kant. Detta är endast 36 % av full kapacitet (jämfört med tidigare formel). Resultatet kan användas för att beräkna inverkan av en lång uppvattnande spricka eller då man av någon anledning (t.ex muddring från isen) måste stå vid en uppsågad vak.
Bild av isborr, hanterad av författaren.
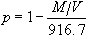
där M är provets vikt (kg) och V är volymen (m3) vid 0°C .Alternativt kan man mäta porvolymen genom att smälta isen i t.ex perkloretylen och fånga gasbubblorna i ett uppochnervänt mätglas.
I fält kan man prova den aktuella böjhållfastheten genom att såga ut balkar direkt i sjöisen. Böjhållfastheten B erhålls ur sambandet
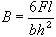
där F är maximal last på avståndet l från inspänningen, b är balkens bredd och h är istjockleken. Längden l bör vara ca 7 gånger istjockleken för att resultatet ska vara jämförbart med tidigare provningar. I tabell 2 redovisas några resultat från balkprovningar på sjö- och älv-is.
Tabell 2.
--------------------------------------------------------------------------------
Källa istyp tvärsnitt (b.h) B antal
--------------------------------------------------------------------------------
Drouin & Michel (1971) älv-is 1000 cm2 5 kg/cm2 14
Gow m.fl (1978) sjö-is 1000 5 55
Fransson (1984) skärgårds-is 5000 2.8 6
sjö-is 1500 4.2 15
konstfrusen is 75 8.4 20
--------------------------------------------------------------------------------
Värdet på B verkar vara mindre för tjock is jämfört med tunn is. Det kan bero på att isytan spricker upp allteftersom den utsätts för temperaturväxlingar. Den spröda kärnisen är också känslig för belastningshastigheten. En balk kan lätt belastas till brott inom någon sekund. En tjock isplatta däremot kan inte böjas till brott lika snabbt. Tyvärr har jag inte funnit några andra resultat i litteraturen som visar hur värdet på B varierar med istjocklek och belastningshastighet.
Beräkna istjockleken 10 dagar efter isläggning då dygnsmedeltemperaturen är -10°C alla dagar.
Lösning:
Istjockleken kan bestämmas med hjälp av sambandet
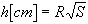
där R väljs till 2.2 med sorterna cm, grader och dygn. S beräknas som summan negativa gader gånger dygn vilket blir
.
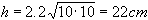Den aktuella istjockleken har uppmätts till 22 cm. Hur stor är då den förväntade istillväxten efter ytterligare 10 dygn om temperaturen förblir konstant lika med -10°C ?
Lösning:
Istjockleken 22 cm motsvarade 100 grad-dygn (se exempel 1).
Den totala istjockleken blr då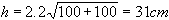 
.
Istillväxten blir alltså 31-22 = 9 cm.
Vilken istjocklek krävs enligt den enkla tumregeln för att nätt och jämnt (otillräcklig säkerhetsmarginal) bära en person på 80 kg.
Lösning:
Tumregeln ger lasten 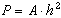där konstanten A väljs till 10 kg/cm2. Vi kan då ur formeln beräkna istjockleken som 
.
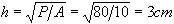Beräkna en trolig brottlast för 3 cm felfri kärnis. Belastningen påförs isen
a) med spetsen av en skridskoskena
b) med foten
c) liggande på magen
Lösning:
Brottlasten beräknas enligt Panfilovs formel
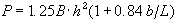. Antag en hög böjhållfasthet som t.ex B = 8.5 kg/cm2 och 
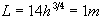. Vi erhåller då följande brottlaster:
a) b = 0, P = 95 (1 + 0 ) = 95 kg
b) b = 0.1 m, P = 95 (1 + 0.08) = 103 kg
c) b = 0.5 m, P = 95 (1 + 0.42) = 135 kg.
Beräkna den minsta istjocklek en isväg av god kvalitet kan ha för att kunna traffikeras med en personbil typ Saab 9000.
Lösning:
Problemet visar sig vara ganska knivigt eftersom många variabler förutom istjocklek inverkar. Isvägens bärförmåga reduceras avsevärt genom den dynamiska belastningen som varierar med fordonets hastighet. Jag gjorde därför ett dataprogram baserad på Panfilovs formel och resonanssvängning där bl.a fordonsvikt, hastighet,hjulbredd, vattendjup, istjocklek och temperatur ingår som indata. Man kan med detta program prova sig fram (se figur) till en lämplig minsta istjocklek på 20 cm. (På grund av normal variation av isens tjocklek och kvalitet bör medeltjockleken vara något större än 20 cm för att lämpa sig för fri fart med en personbil.)
