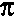Tekniska Högskolan i Luleå

avd Konstruktionsteknik

Strength of warm porous ice in the Gulf of Bothnia

Field investigation.

Lennart Fransson and Lars Åström, Luleå University of Technology, Sweden

Jan-Erik Lindholm, Helsinki University of Technology, Finland

Abstract

When ice is crushed in a brittle manner as in most strength tests we assume that elasticity, fracture energy and sample size governs the result. For porous ice measured uniaxial strength was reduced due to the average size of the air bubbles and the assumed pre-existing cracks. The strength of porous granular ice was calculated from measured bulk density and earlier measured fracture toughness on pure ice. In general, a falling trend was traced as predicted with the presented formula although the scatter of the field data was large. Ice strength obtained from pressure-meter tests was comparable with those from the uniaxial compression tests when they were carried out shortly after sampling. The crystal analysis was supported with a video-camera which made it faster.

Introduction

The winter of 1991/92 was very mild in the Bothnian Bay, in fact the mildest during the whole 20th century, Lundqvist (1992). In March when the study began Luleå harbour was ice-free and all pack ice was compressed on the Finnish coast and at the very north of the Bay. In general it was not the best winter for ice research.

The field program was carried out in cooperation by Luleå and Helsinki University of Technology from the Finnish research vessel RV Aranda. The aim of this report is to present representative strength data at the given ice situation to be used in ice force calculations.

Strength data on brackish ice from the Gulf of Bothnia, measured with similar technique, have earlier been published (Fransson, 1987),(Fransson et.al., 1990). This report provides new information about soft warm ice measured immediately before ice ridging. Strength data and more results from the field study such as pressure ridge data can be found in the report "Field measure-ments of Northern Baltic pressure ridges." by Reynolds and Lindholm (1992). See map on the ice situation 1992-03-12 in the Gulf of Bothnia.

Test methods

During warm weather the mechanical properties of ice drastically change with temperature. In order to minimize such unwanted side effects the ice was tested in situ (pressure-meter tests) or immediately after sampling (Uniaxial compression tests). Large vertical cores through the ice cover were sampled close to RV Aranda. On board in a coldroom (set close to the melting temperature) small cylindrical specimen were prepared from the core at different depths. The volume and weight of each cylinder was measured and thin sections were examined in cross-polarized transmitted light. Some work in the coldroom and in the field was documented on video.

Uniaxial compression tests were carried out with a small but stiff loading machine on 70 mm cylindrical specimen. The loading machine was operated by a manual hydraulic pump on which each stroke moved the indentor 0.6 mm. A typical speed of 1 stroke per second was used but the effective indentation speed was reduced by the deformation of two 4 mm rubber pads at the interfaces. The time to failure was in most cases within the range 5-10 seconds.The ice was often very porous and sometimes large pores totally sabotaged the strength. Even though the ice was weak it was brittle and the peak load was limited by instability of the sample. The measured peak load divided by the cross sectional area is presented as the uniaxial compressive strength at a specified field station and ice depth.

In the central part of the station pressuremeter tests were carried out in order to get a rough approximation of the in-situ compressive strength. In the pressuremeter tests the ice cover was drilled through with a 60 mm ice auger. Then a rubber membrane was placed in the bore-hole and expanded with a liquid until the ice was locally crushed. The tests were usually carried out at six spots only a few meter from each other. The result can therefore be considered as an average index strength of a relatively large volume of ice. In Figure 1 the pressuremeter test set up is shown.

Test Result

Weather and ice condition

Air temperatures during the testing period were unseasonable warm, ranging from +4°C to -10.6°C. Southern winds had pushed snow-mixed ice up to the very north of the Bothnian Bay where our tests took place. Ice strength tests were done at six different stations (A-F) during 12-17 March 1992. Station A and B was on granular ice with the temperature at the melting point. The top layer was harder and less deteriorated. Station C was on a thin granular ice sheet at -0.4°C. Station D was on a 80 cm thick ice floe nearby a pressure ridge. The ice was a mixture of various granular types with large air inclusions and overlaid by thin level ice. Station E was on the land fast ice cover close to the Finnish coast at Marjaniemi which consisted of well consolidated granular snow-ice. Finally, station F was on a small ice floe with melting mixed ice where the center portion contained thin broken columnar ice. Weather and ice conditions are given in Table 1.

Table 1. 

---------------------------------------------------------------------------
 Date     Field         GPS       Air Temp    Wind Speed    Ice Conditions    
March    Station     Position      °C          m/s             h = ice       
 -92                             High   Low   High    Low      thickness      
---------------------------------------------------------------------------
  10        -            -       +4.0   +0.7  14.9    6.7     open water      
  11        -            -       +1.1   -0.3  16.3    6.4    brash barrier    
  12       A, B     65:23.97 N   +0.5   -2.8  19.7    4.9    consolidated     
         Malören    23:34.22 E                              floes h=40-60cm   
  13        C       65:24.86 N   +0.4   -0.6  18.2    4.2    level ice and    
         Malören    23:31.39 E                               ridges h=12cm    
  14    D  Malören  65:15.08 N   -0.5   -2.9  12.8    0.5   ice floe h=80cm   
                    23:34.40 E                              with 10 cm snow   
  15    D  Malören  65:15.08 N   -1.1   -5.5   7.7    0.8   as 14/3 with 5    
                    23:34.40 E                                 cm slush       
  16        E       65:02.32 N   -0.5  -10.6   7.1    1.3       landfast       
        Marjaniemi  24:32.67 E                              snow-ice h=70cm   
  17        F       65:24.98 N   -0.7   -5.4  15.1    5.5   ice floe h=45cm   
         Malören    23:34.81 E                              with 5 cm slush   
  18     Malören    65:24.06 N   +0.3   -1.4  17.7    5.4     level ice,      
                    23:34.05 E                              ongoing ridging   
---------------------------------------------------------------------------

Uniaxial compressive strength

A total of 87 samples were measured and tested. The average strength of the warm granular and mixed ice was 1.5 MPa when loaded horizontally. In Figure 2 the average strength for all stations are shown. At station F some specimen were cut with horizontal Fh , vertical Fv and 45 degree loading direction F45. The strength was about the same in all direction which means no clear anisotropy within a specified depth (20 cm).

Figure 3 shows ice depth vs. horizontal strength for all tested samples. The thinner ice (B and C) was stronger with an average strength of 3.0 MPa. In general the top layer was stronger than average. The depth dependency was however masked by the large scatter. All the basic data is given in more detail in appendix.

Crystal analysis

The crystal structure of the remaining of the ice cores was examined in cross-polarized transmitted light and in reflecting light in order to visualize both the crystal structure and the shape of the air bubbles. In Figure 4a, b and c representative vertical sections are shown. Ice type, grain size and air bubble sizes are given in the figure text. Figures 5 and 6 show a complete vertical section through the ice at F. When the thin sections were magnified in a microscope the shape and size of small bubbles and brine pockets could be studied. In Figure 7 hardcopies from a study, videotaped through the ocular, are shown.

Pressuremeter strength

The ice thickness was often too small to be measured with the pressure-meter which has an effective probe length of about 20 cm. Even when the ice was thick enough the extremely high porosity (up to 20 %) made the evaluation somewhat arbitrary. The drop of pressure was unclear and sometimes there was a need of a larger expansion than was allowed In the Table the pressuremeter data is compared with the average uniaxial strength at the same station and depth. According to Michel (1983) the pressuremeter strength can be converted to an index strength by dividing the value with an constant (= 2.5 for granular ice).

Table 2. 

---------------------------------------------------------------------------
Station     Ice    Test   Pressuremeter  Pressuremeter  Uniaxial  
          Depth   Depth     Strength     Strength/2.5   Strenght  
           (cm)    (cm)       (MPa)          (MPa)       (MPa)    
---------------------------------------------------------------------------
   A        50      20         3.2            1.3         1.8    
          +/- 8     35         2.5            1.0         1.4                 
   B        25      10         4.8            1.9         3.5     
          +/- 7                                                   
   D        78      20         1.7            0.7         0.55    
          +/- 3     40         2.6            1.0         1.51    
                    60         3.7            1.5         1.61    
   F        44      20         2.5            1.0         1.85    
          +/- 4                                                   
---------------------------------------------------------------------------


Density and salinity

Weight and volume was accurately measured on the cylindrical specimen which had an constant diameter of 70.0 mm. The density was calculated as

= M / (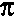LD2/4) ... (1)

where M is weight, L is length and D is diameter of the specimen. Using the measured density the porosity p was defined

p = 1 - 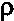/ 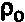... (2)

where 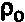is the density of pure ice (= 920 kg/m3).

Salinity of the water of melted samples was estimated from conductivity measurements in room temperature. The low salinity (0.02 - 0.2 o/oo) and the ongoing melting in the field made the salinity measurements inaccurate and consequently calculations of brine volume would be misleading. In melting conditions tubular voids may be water filled which also affects the porosity measurements. In Figure 8 porosity and salinity profiles at different stations are shown.

Strength-porosity relationship

The porosity dependence of uniaxial strength can be studied by assuming that the ice is crushed in a brittle manner. From Kendall (1978) we obtain the splitting load

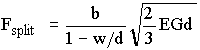... (3)

where b and d are the cross section dimensions and w/d is the effective contact width at the loading face of the specimen. E is the elastic modulus and G is the fracture surface energy. The porosity dependence of elastic modulus in brittle solids has been analysed by Krstic and Erickson (1987) based on crack opening displacement. A round specimen with spherical pores will according to Krstic and Erickson have the effective modulus

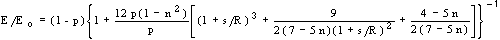... (4)

where Eo is elastic modulus for pure ice, p is porosity, 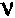is Poisson's ratio and s/R is a relative crack length close to a spherical pore. In ice the shape of a newly formed air bubble has an elongated form which later tend to be more spherical. Therefore it is reasonable to assume a crack length of the same order as the bubble radius. With s/R = 1 and 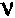= 1/3 in Eq. (4) we obtain

E/Eo = (1-p)/(1+30p). ... (5)

Fracture energy is usually scaled linearly with the fractured area which perpendicular to cylindrical bubbles results in

G/Go = 1-p. ... (6)

In the case of large pre-existing cracks in the fracturing direction also s/R will have an influence on the fracture energy. It is not obvious how the shape of the air bubbles should be included in the formula and therefore Eq. (6) is applied even for our spherical bubbles. A substitution of Eqs. (5) and (6) into Eq. (4) results in a porosity dependent effective pressure of

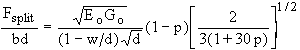... (7)

In the linear fracture mechanics theory 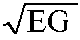is equal to the critical stress intensity Kic which is experimentally evaluated for sea ice from the Gulf of Bothnia. In our case Kic = 100 kPa m1/2 is a possible value for pure granular ice, Stehn (1990). With almost constant sample dimensions l/D = 2.4 the relative contact width is considered as constant w/d = 0.9. Equation (7) is then rewritten

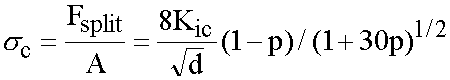... (8)

where c is the uniaxial "compressive strength" which as well could be named "splitting strength". Using Kic = 100 kPa m 1/2 and d = D = 0.07 m results in a strength of 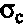= 3.0 MPa. This is a relatively low value which indicate that the relative contact width may be greater than 0.9. In this early stage of the use of Eq. (8) there is no meaning in adjusting w/d just to get a better fit. In Figure 9 measured and calculated strength is plotted as a function of porosity.

A falling trend can be traced even though the strength of low porosity ice was very scattered. One important reason for that may have been that mixed ice types with different degree of deterioration was involved.

Discussion

It is natural to expect a clear strength-density dependency for porous ice. It is not easier to measure density than index strength but the presented formula may still be useful. Lake ice and river ice can be almost bubble free with a density close to pure ice. The formula makes it possible to extrapolate obtained strength data of a granular ice type to the worst case as in a design situation.

The size distribution of air bubble inclusions is not considered in the proposed formula. Large bubbles will have a dramatic influence of the density but not necessarily on the strength. Small bubbles and elongated bubbles play a more important role if they form weakness plane. Therefore it makes sense to analyse the air bubble distribution and at least separate cylindrical bubbles from spherical. In many cases the air bubbles are closely linked to the actual ice type but at warm temperatures the patterns will change rapidly from cylindrical towards spherical.

The testing procedure worked well although the ice was in a melting condition. When the ice was tested immediately after sampling on board the ice-breaker the result was consistent with those from the in situ testing. In most situations in situ testing seem to be good enough to classify ice strength if also salinity, density and temperature is measured. When strength tests are performed on small porous samples, mapping of the pore geometry of each sample is motivated.

The use of a video-camera for examination and documentation of crystal structure and pore geometry worked smoothly. Even though the quality of prints was poor it was a practical complement to ordinary photos.

References

Fransson, L. (1987) Horizontal compressive strength of low salinity ice from the Gulf of Bothnia. Proceedings from the 9th Int. conf. on Port and Ocean Engineering under Arctic Conditions (POAC-87), Fairbanks, Alaska, Vol. III, pp 21-29.

Fransson, L., Håkansson, B., Omstedt, A. and Stehn, L. (1990) Sea ice properties studied from the icebreaker Tor during BEPERS-88. Rep. SMHI RO No. 10, Norrköping Sweden, 20 p + 3 attachments.

Kendall, K. (1978) Complexities of compression failure. Proc. Royal Society of London. A 361, pp 245-263.

Krsic, V. D. and Erickson, W. H. (1987) A model for the porosity dependence of Young's modulus in brittle solids based on crack opening displacement. Journal of Materials Science No. 22, pp 2881-2886.

Michel, B. C. (1983) Final report - Development of a field technique to measure the in situ crushing strength of ice, Phase II. Report to Marine Aids Civil, Transport Canada, 66 p. + 6 annexes.

Reynolds, E. and Lindholm J-E. (1992) Field measurements of Northern Baltic pressure ridges. Rep. M-19, Arctic Offshore Research Centre, Helsinki University of Technology, 32 p.

Stehn, L. (1990) Fracture toughness of sea ice - Development of a test system based on chevron notched specimen. Licentiate Thesis 1990:11L. Division of Structural engineering, Luleå University of Technology, 88 p.

Appendix

Test Data 12-17 March 1992

The data is given in the following units:

depth     density     salinity     measured load     strength
(cm)      (kg/m3)      (o/oo)         (V)             (MPa)

Average strength and standard deviation for each station A-F is given in the two last columns. The identification of a single horizontal sample is given by Station-No and depth from the ice surface in cm (e.g. sample D2-30 with a strength of 1.84 MPa). The presented strength was obtained from uniaxial loading tests on cylindrical specimen with a diameter of 70 mm and a height varying from 160 to 177 mm. The temperature of the specimen was close to the melting point 0 °C.